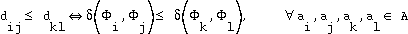2.3 Mapping cyberspace over a visualization media

2.3.3 Metrics

A contrasting approach is to define a requirement based on the distance among elements. This approach clearly gives more freedom, but also increases the computational complexity since the transformation will now be based on the distance matrix.

Suppose that the goal of the transformation has a central feature of obtaining a monotone relationship between distances. Then only the rank order of the dissimilarities has to be preserved by the transformation. Hence, the metric is abandoned during the mapping. Therefore the transformation must obey the monotonicity constraint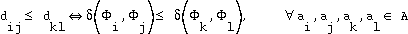
.

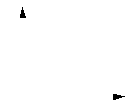monotonicity satisfied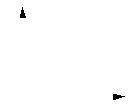

monotonicity not satisfied

 

If the metric nature of the transformation is to be preserved, a configuration will have to satisfy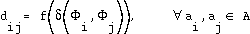

where is a monotonic function of the distance; a possible straighforward example could be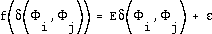
.

The stronger constraint that we can put on the mapping is the isometry, having then a perfect preservation of the topology. An isometry is defined by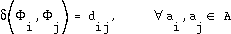
.

It is obvious that a mapping that satisfies the isometry also conserves the monotonicity among distances.

Cyberspace geography visualization - 15 October 1995

Luc Girardin, The Graduate Institute of International Studies