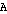 to set
to set 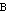 is a mapping that has a corresponding relation tuple (element) in
is a mapping that has a corresponding relation tuple (element) in 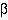 for each relation in
for each relation in 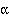 . A mapping fulfilling this requirement is called a homomorphism from
. A mapping fulfilling this requirement is called a homomorphism from 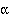 to
to 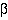 such that
such that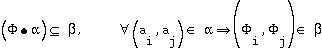 .
.



2.3 Mapping cyberspace over a visualization media
An exact match from the set 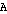 to set
to set 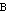 is a mapping that has a corresponding relation tuple (element) in
is a mapping that has a corresponding relation tuple (element) in 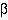 for each relation in
for each relation in 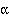 . A mapping fulfilling this requirement is called a homomorphism from
. A mapping fulfilling this requirement is called a homomorphism from 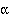 to
to 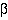 such that
such that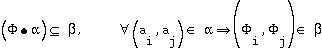 .
.
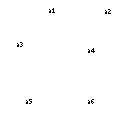 | 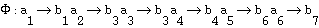 | 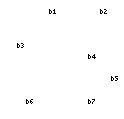 |
Consider that a mapping exists wherein there is a one-to-one correspondence between the vertices in 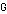 and the vertices in a subgraph of
and the vertices in a subgraph of 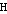 such that a pair of vertices are adjacent in
such that a pair of vertices are adjacent in 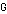 if and only if the corresponding pair of vertices are adjacent in the subgraph of
if and only if the corresponding pair of vertices are adjacent in the subgraph of 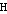 . This is in fact the condition for a monomorphic mapping:
. This is in fact the condition for a monomorphic mapping:
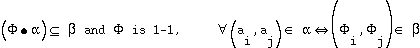
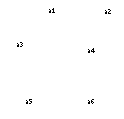 | 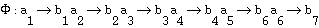 | 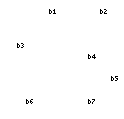 |
which can also be described as a isomorphic mapping to a subset 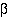 from the relation
from the relation 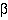 such that
such that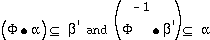 .
.
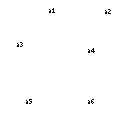 | 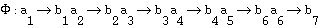 |  |
Note that all these morphism problems have been shown to be NP-complete and therefore cannot be solved exactly in polynomial time.