2.1 Cyberspace representation
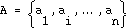of 
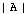resources with a relation 
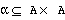between pairs 
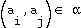of linked resources. It is possible to model this system with a connected graph 
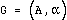where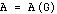 
represent the vertices (nodes) and 
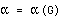the edges (undirected arcs) between vertices of the graph. The size of 
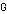is the number of edges, thus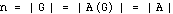 
 |
The information in the graph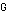 
may also be expressed in a variety of ways in matrix form. There is one such matrix, the adjacency matrix, that is especially useful. An adjacency matrix 
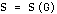of the graph 
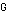is of size 
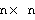. The entries in the adjacency matrix, 
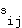, records which pairs of nodes are adjacent. If nodes 
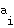and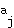 
are adjacent, then 
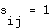, and if nodes 
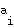and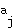 
are not adjacent, then 
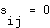. The entries on the diagonal, values of 
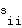, are undefined, because we do not allow loops in the graph.
  |
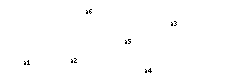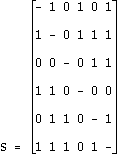The following elements are introduced to extract features and components of the graph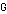 
:
:
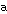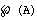denotes the set of the parts of 
;
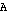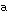, which is the number of edges incident to the vertex. In the adjacency matrix the nodal degrees are equal to either the row sums or the column sums. This degree can be seen, for our purposes, as a characteristic of a resource.
.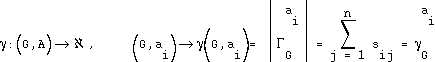